674.最长连续递增序列

给定一个未经排序的整数数组，找到最长且 连续递增的子序列，并返回该序列的长度。

连续递增的子序列 可以由两个下标 l 和 r（l < r）确定，如果对于每个 l <= i < r，都有 nums[i] < nums[i + 1] ，那么子序列 [nums[l], nums[l + 1], ..., nums[r - 1], nums[r]] 就是连续递增子序列。

示例 1:

输入：nums = [1,3,5,4,7]
输出：3
解释：最长连续递增序列是 [1,3,5], 长度为3。
尽管 [1,3,5,7] 也是升序的子序列, 但它不是连续的，因为 5 和 7 在原数组里被 4 隔开。

示例 2:

1
2
3

输入：nums = [2,2,2,2,2]
输出：1
解释：最长连续递增序列是 [2], 长度为1。

提示:

1 <= nums.length <= 10^4
-10^9 <= nums[i] <= 10^9

来源：力扣（LeetCode）

链接：https://leetcode.cn/problems/longest-continuous-increasing-subsequence/description/

思路

这一题贪心和动态规划的代码几乎差不多，因为动态规划就是通过递推表达式来确保局部的最优，最后推出结果，贪心也同样是局部推出最优。当动态规划的dp数组可以降为一个数的时候，他们的代码将几乎一致。

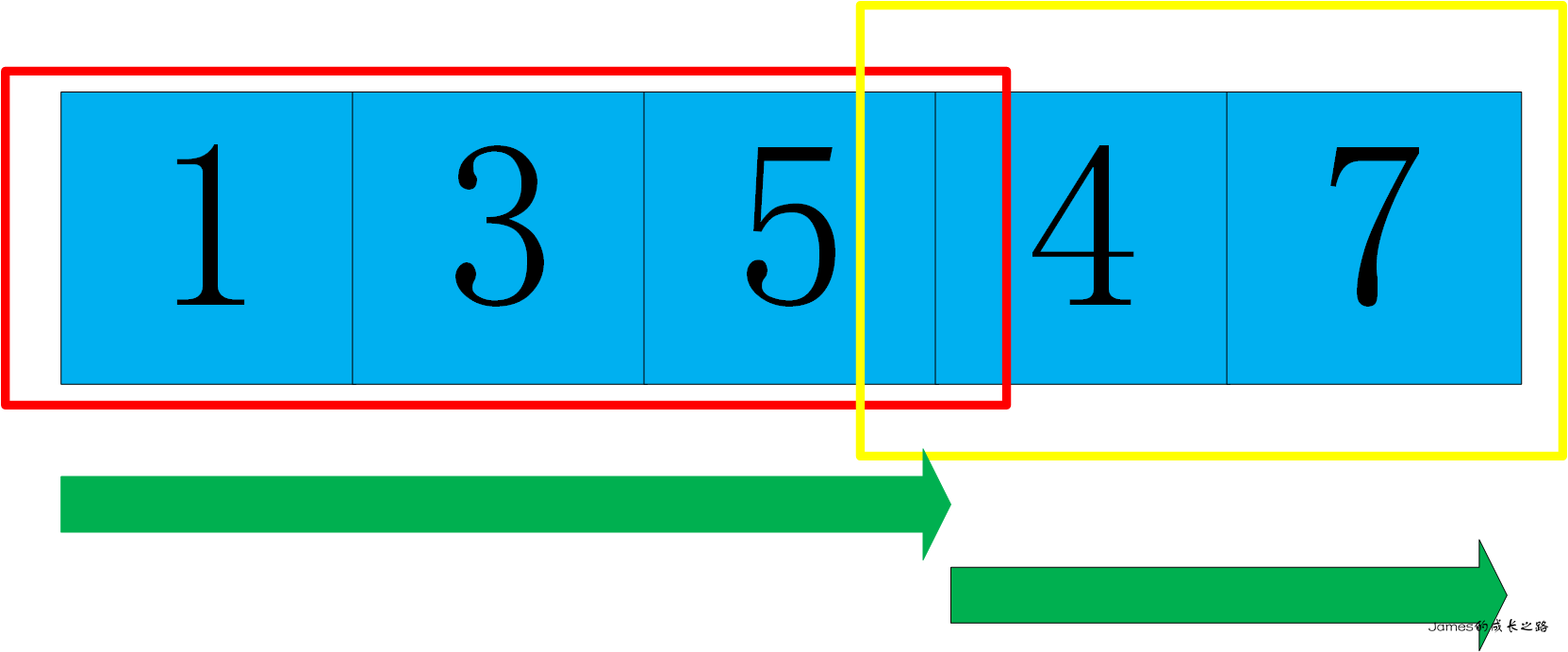
很容易看出，贪心的思路将是从前到后遍历，当nums[i]>nums[i - 1]就计数+1，否则重置为0重新计数。

从动态规划的角度出发，我们将dp数组定义为：dp[i]以下标i为结尾的连续递增子序列的长度。递推公式很容易看出如果nums[i]>nums[i - 1]，dp[i] = dp[i - 1] + 1。dp数组的初始化也可以知道当每个递增序列只有自己时长度为1 ，故初始化为1。这里由于后面的状态依赖于前面的状态所以从前向后遍历。

然而，这里每次递推时只用到前一个状态，我们可以只用一个数来作为dp数（组），这时初始化就应该在不满足递增时初始化，可以很容易的写出代码。会发现两种方式写出的代码一模一样！

实现代码

动态规划：

class Solution {
public:
    int findLengthOfLCIS(vector<int>& nums) {
        int dp = 1;
        int res = 1;
        for(int i = 1; i < nums.size(); ++i){
            if(nums[i] > nums[i - 1])
                dp++;
            else dp = 1;
            res = max(res, dp);
        }
        return res;
    }
};