《代码随想录》笔记2——算法性能分析
本文是我在学习(程序员Carl (opens new window))的原创作品《代码随想录》做的笔记。现上传到我的博客,大家可以去看看大佬的作品,真的很不错。
算法性能分析
时间复杂度
时间复杂度
(1)时间复杂度
一个函数,定性描述一个算法的运行时间。
假设算法的问题规模为n,那么操作单元数量便用函数来表示,随着数据规模的增大,算法执行时间的增长率和的增长率相同,这称作为算法的渐近时间复杂度,简称时间复杂度,记为 。
(2)大O
函数的渐近上界。
输入数据的形式对程序运算时间是有很大影响的,在数据本来有序的情况下时间复杂度是O(n),但如果数据是逆序的话,插入排序的时间复杂度就是,也就对于所有输入情况来说,最坏是的时间复杂度,所以称插入排序的时间复杂度为。快速排序是,但是当数据已经有序情况下,快速排序的时间复杂度是的,所以严格从大O的定义来讲,快速排序的时间复杂度应该是。但是我们依然说快速排序是的时间复杂度,这个就是业内的一个默认规定,这里说的代表的就是一般情况,而不是严格的上界。
(3)不同数据规模下不同时间复杂度的时间
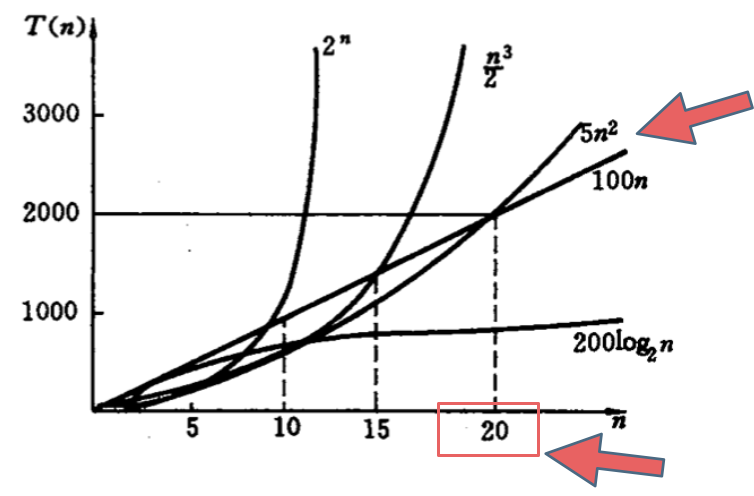
从上图可以只看出再决定使用什么算法时,并不是时间复杂度越低越好,这和输入数据的规模有很大的关系。为什么会出现这种情况呢?这就关系到大的定义**:数据量级突破一个点且数据量级非常大的情况下所表现出的时间复杂度,这个数据量也就是常数项系数已经不起决定性作用的数据量**。
通常时间复杂度的排序如下:
注意这里的不一定以2为底,这是忽略底数的描述。
计算机的性能决定算法花费的时间
计算机的运算速度主要看CPU的配置,以2015年MacPro为例,CPU配置:2.7 GHz Dual-Core Intel Core i5 。也就是 2.7 GHz 奔腾双核,i5处理器,GHz是指什么呢,1Hz = 1/s,1Hz 是CPU的一次脉冲(可以理解为一次改变状态,也叫时钟周期),称之为为赫兹。
- 1GHz(兆赫)= 1000MHz(兆赫)
- 1MHz(兆赫)= 1百万赫兹
所以 1GHz = 10亿Hz,表示CPU可以一秒脉冲10亿次(有10亿个时钟周期),但是并不是一个时钟周期就是一次CPU运算。
例如1 + 2 = 3,cpu要执行四次才能完整这个操作,步骤一:把1放入寄存机,步骤二:把2放入寄存器,步骤三:做加法,步骤四:保存3。而且计算机的cpu也不会只运行我们自己写的程序上,同时cpu也要执行计算机的各种进程任务等等,我们的程序仅仅是其中的一个进程而已。
递归的时间复杂度
同一个问题可以写出和的代码。这里有一些例子。求x的n次方。
****的直观算法
1 | int function1(int x, int n) { |
****的递归算法1
1 | int function2(int x, int n) { |
递归算法的时间复杂度的本质是递归的次数*每次递归的操作次数。这里每次递归进行一次一次乘法操作,所以时间复杂度是。
****的递归算法2
1 | int function3(int x, int n) { |
这里的时间复杂度需要根据递归树来计算,以n=16为例:
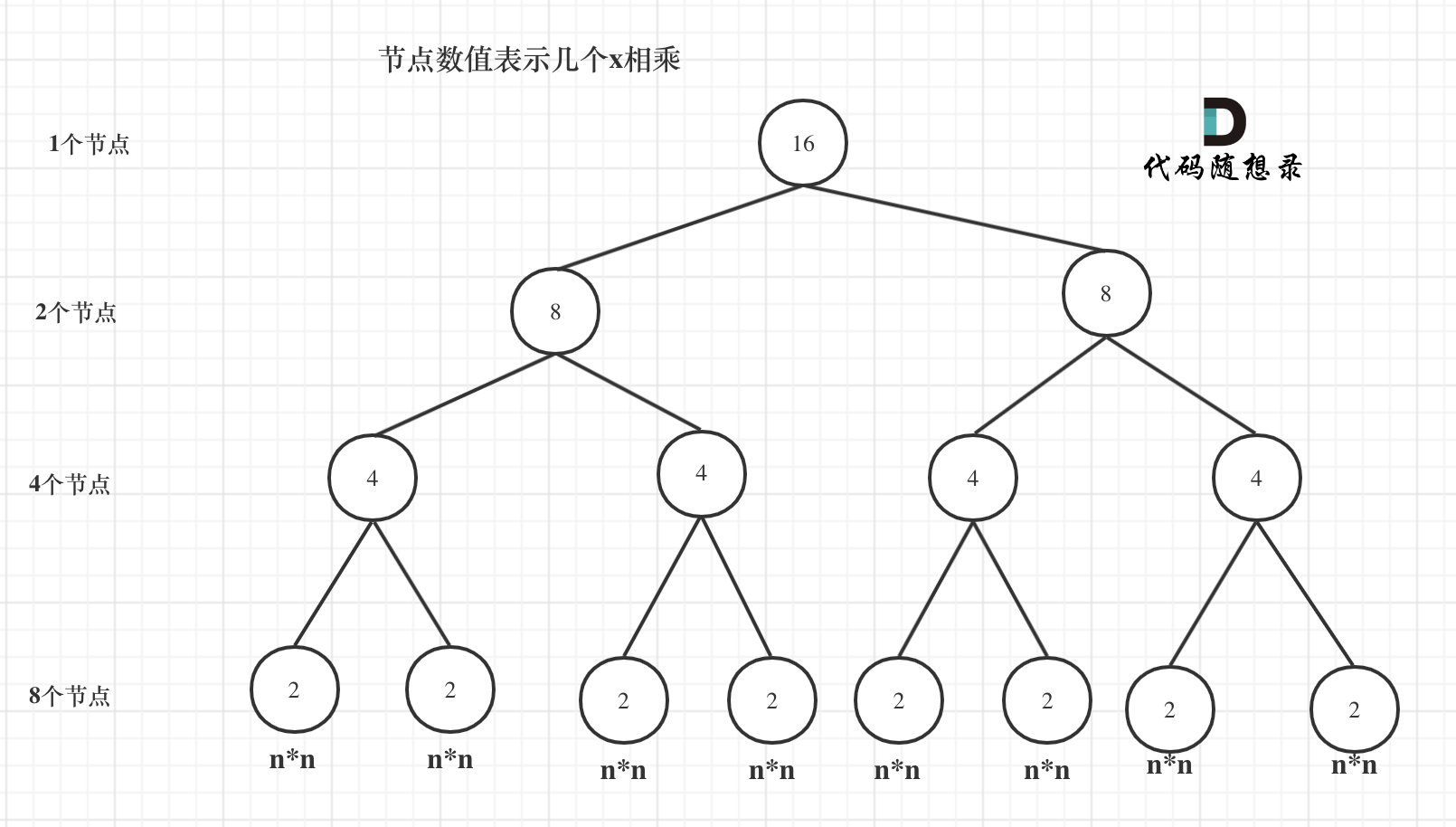
这颗满二叉树的节点数量是。
**若满二叉树的深度为(从0开始),则有个节点,其中。**故忽略常数项-1后,时间复杂度为。
的递归算法
1 | int function4(int x, int n) { |
这里把相同的递归调用提取出来只进行一次递归,保存副本值用于后面的计算,乘法次数为递归树的高度,大大提高了效率。
空间复杂度
空间复杂度
对算法在运行过程中占用内存空间大小的量度,记做。用来对程序运行中需要的空间进行估计。编译器的内存对齐,编程语言容器的底层实现等都会影响程序真正的内存开销。
的空间复杂度
1 | int j = 0; |
程序开销的内存不会随的变化而变化。表示为。
的空间复杂度
1 | int* a = new int(n); |
消耗空间和输入参数n保持线性增长,这样的空间复杂度为O(n)。
递归算法的时间与空间复杂度分析
递归求斐波那契数列的性能分析
1 | int fibonacci(int i) { |
时间复杂度和空间复杂度分析
以为例,递归树如图:
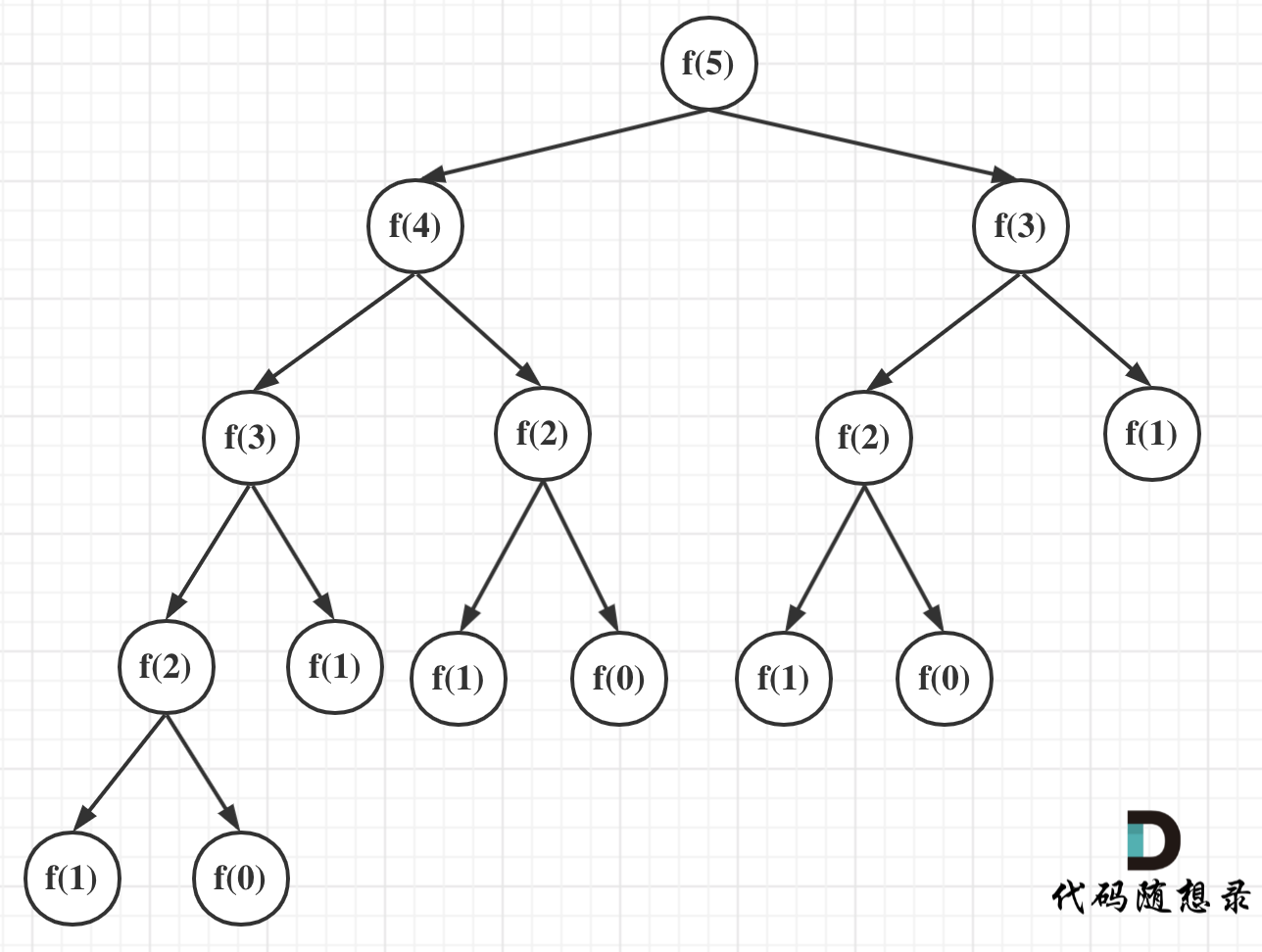
由于一棵二叉树的深度为(根节点深度为1)可以有个节点。故时间复杂度为。
递归算法的空间复杂度 = 每次递归的空间复杂度 * 递归深度
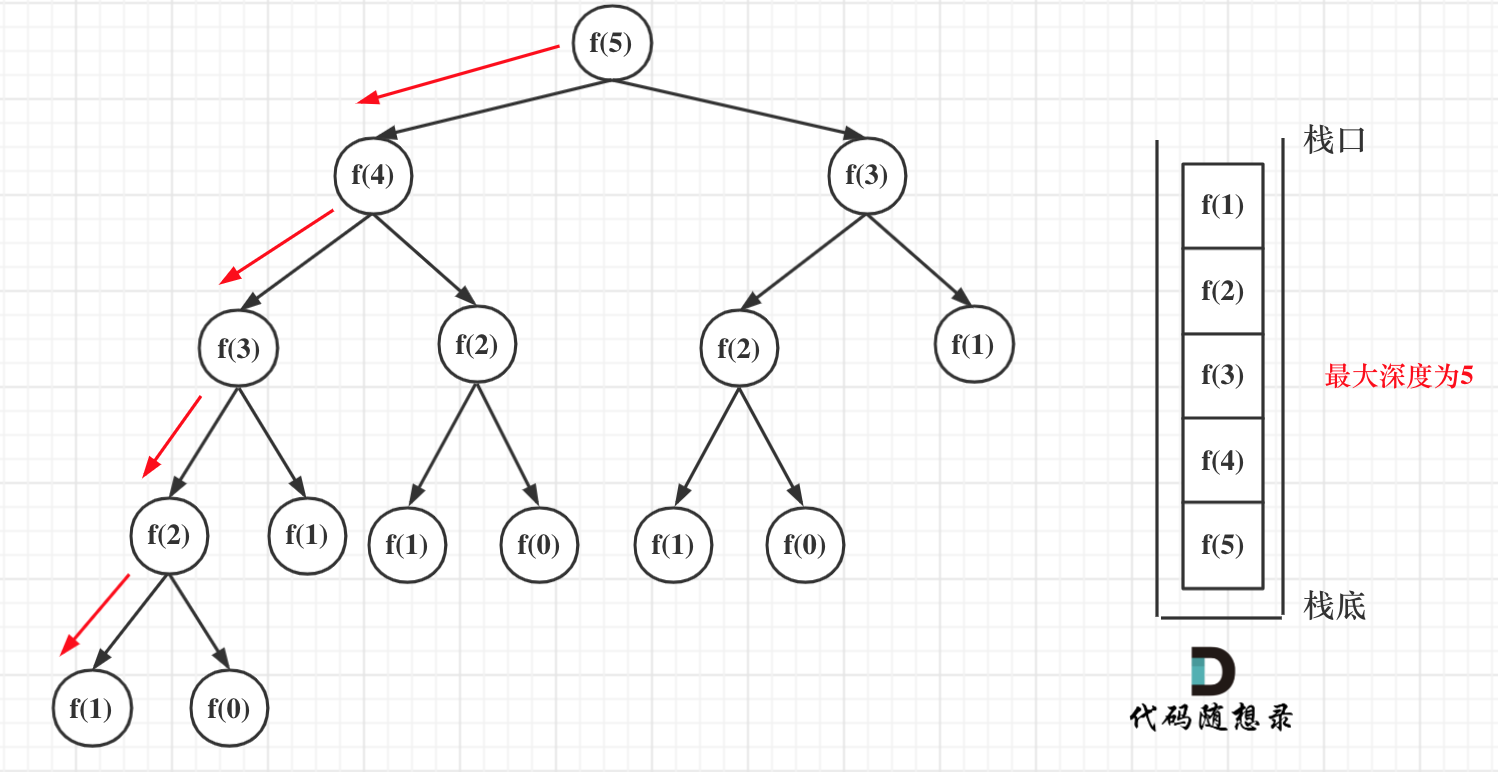
由于每次递归都需要栈里,到达递归最深处时就开始弹出,又每次递归需要常数空间,所以空间复杂度为。
1 | // 版本二 |
使用first和second来记录当前相加的两个数值,减少递归次数。故时间复杂度为,又递归的深度是n,每次递归需要常数空间,所以空间复杂度为。
内存消耗
不同语言的内存管理
不同的编程语言各自的内存管理方式。
- C/C++这种内存堆空间的申请和释放完全靠自己管理
- Java 依赖JVM来做内存管理,不了解JVM内存管理的机制,很可能会因一些错误的代码写法而导致内存泄漏或内存溢出
- Python内存管理是由私有堆空间管理的,所有的python对象和数据结构都存储在私有堆空间中。程序员没有访问堆的权限,只有解释器才能操作。
C++的内存管理
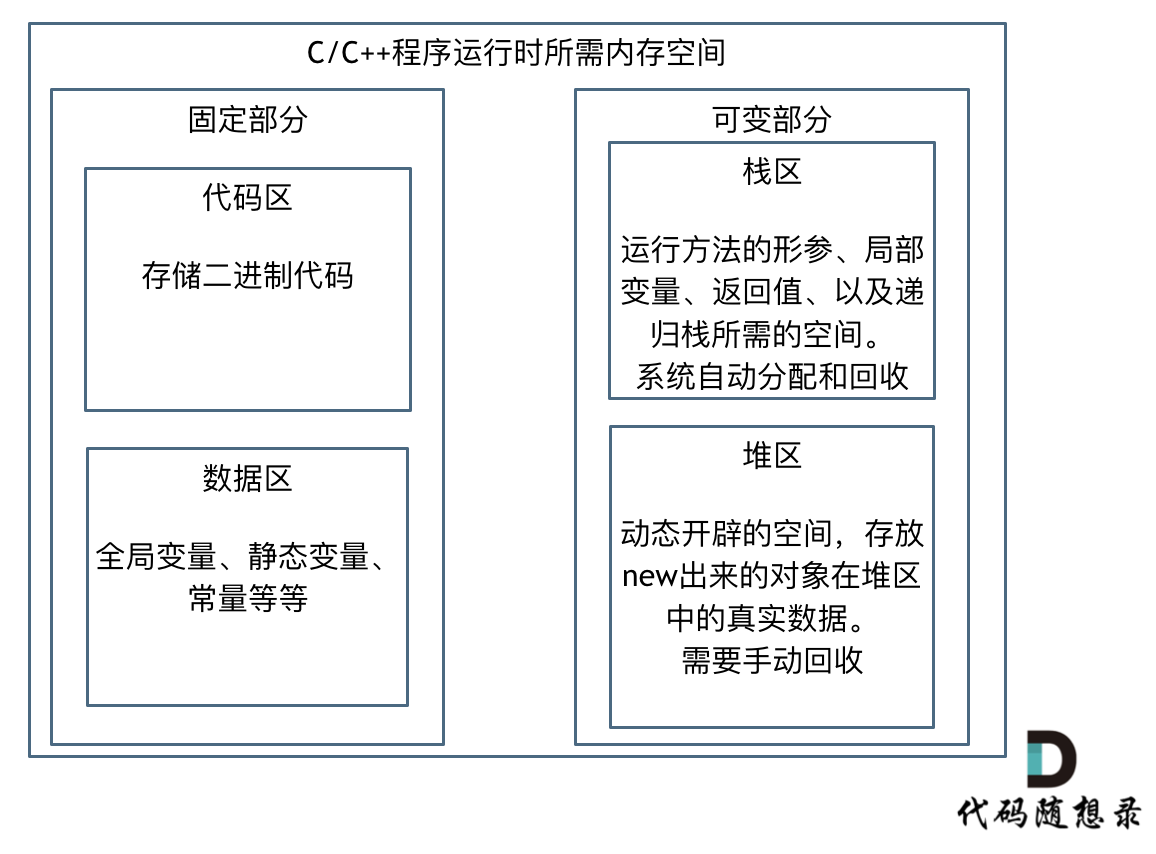
固定部分的内存消耗是不会随着代码运行产生变化的, 可变部分则是会产生变化的。
由C/C++编译的程序占用的内存分为以下几个部分:
- 栈区(Stack) :由编译器自动分配释放,存放函数的参数值,局部变量的值等,其操作方式类似于数据结构中的栈。
- 堆区(Heap) :一般由程序员分配释放,若程序员不释放,程序结束时可能由OS收回
- 未初始化数据区(Uninitialized Data): 存放未初始化的全局变量和静态变量
- 初始化数据区(Initialized Data):存放已经初始化的全局变量和静态变量
- 程序代码区(Text):存放函数体的二进制代码
代码区和数据区所占空间都是固定的,而且占用的空间非常小,运行时消耗的内存主要是可变部分。在可变部分中,栈区间的数据在代码块执行结束之后,系统会自动回收,而堆区间数据是需要程序员自己回收,所以也就是造成内存泄漏的原因。
计算程序占用内存
基础数据类型大小:

64位的指针就占用8个字节,而2位的指针占用4个字节的原因
1个字节占8个比特,那么4个字节就是32个比特,可存放数据的大小为,也就是4G空间的大小,即:可以寻找4G空间大小的内存地址。64位的操作系统的计算机内存都已经超过了4G,4个字节的指针已经不能寻址全部的内存地址,所以64位编译器使用8个字节的指针才能寻找所有的内存地址。
内存对齐
可以跨平台的编程语言都需要做内存对齐。为什么会有内存对齐?
主要是两个原因
1.平台原因:不是所有的硬件平台都能访问任意内存地址上的任意数据,某些硬件平台只能在某些地址处取某些特定类型的数据,否则抛出硬件异常。为了同一个程序可以在多平台运行,需要内存对齐。
2.硬件原因:经过内存对齐后,CPU访问内存的速度大大提升。
内存对齐的效果:
CPU并不是一次读取单个字节,而是一块一块的读取,块的大小可以是2,4,6,8,16个字节。具体取决于硬件。
假设CPU把内存划分为4字节大小的块,要读取一个4字节大小的int型数据,两种情况下CPU的工作量:
第一种就是内存对齐的情况,如图:
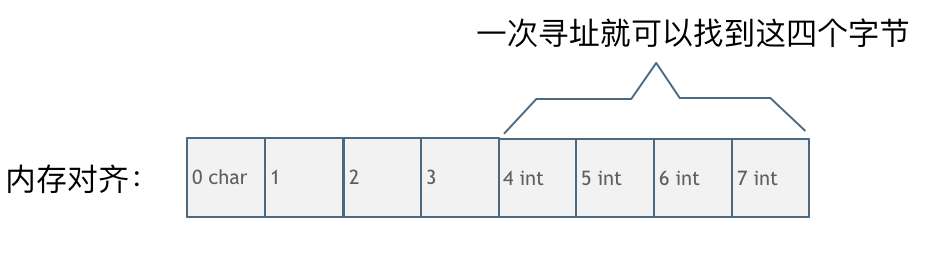
一字节的char占用了四个字节,空了三个字节的内存地址,int数据从地址4开始。此时,直接将地址4,5,6,7处的四个字节数据读取到即可。
第二种是没有内存对齐的情况如图:
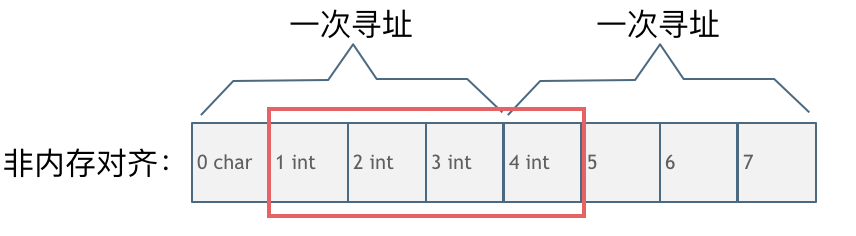
char型的数据和int型的数据挨在一起,该int数据从地址1开始,那么CPU想要读这个数据的话来看看需要几步操作:
1.因为CPU是四个字节四个字节来寻址,首先CPU读取0,1,2,3处的四个字节数据
2.CPU读取4,5,6,7处的四个字节数据
3.合并地址1,2,3,4处四个字节的数据才是本次操作需要的int数据
此时一共需要两次寻址,一次合并的操作。
注:本文的封面图片由wal_172619在Pixabay上发布










