第1章 矢量分析
1.1 矢量代数
1.1.1 标量和矢量
数学上,任一代数量a都可称为标量。在物理学中,任一代数量一旦被赋
予“物理单位”,则称为一个具有物理意义的标量,即所谓的物理量,如电压u电
荷量Q、质量m能量w等都是标量。
一般的三维空间内某一点 P处存在的一个既有大小又有方向特性的量称为
矢量。
单位矢量:模为1的矢量称为单位矢量。eA表示与矢量A同方向的单位矢量,显然:
eA=AA
常矢量:大小和方向均不变的矢量。 单位矢量不一定是常矢量。
1.1.2 矢量的加法和减法
平行四边形法则:
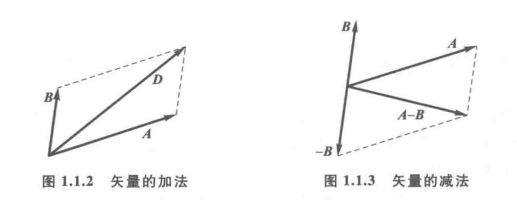
运算法则:
交换律:A+B=B+A
结合律:(A+B)+C=A+(B+C)
1.1.3 矢量的乘法
标量和矢量:kA还是矢量,大小为∣k∣A,k>0,则kA与A同方西,反之。
矢量和矢量:
(1)点积(标积):
交换律:A⋅B=B⋅A
分配律:A⋅(B+C)=A⋅B+A⋅C
(2)叉积(矢积):
显然有:A×B=−B×A
不满足交换律。
分配律:A×(B+C)=A×B+A×C
标量三重积:A⋅(B×C)=B⋅(C×A)=C⋅(A×B)
矢量三重积:A×(B×C)=B⋅(C×A)=C×(A×B)
1.2 三种常用的正交曲线坐标系
电磁理论中,常用直角坐标系,圆柱坐标系和球坐标系。
1.2.1 直角坐标系
右手螺旋定则:ex×ey=ez×ey×ez=ex×ez×ex=ey
任意矢量A表示为:A=exAx+eyAy+ezAz
两矢量和:A+B=ex(Ax+Bx)+ey(Ay+By)+ez(Az+Bz)
两矢量点积:
A⋅B=(exAx+eyAy+ezAz)⋅(exBx+eyBy+ezBz)=AxBx+AyBy+AzBz
两矢量叉积:
A×B=(exAx+eyAy+ezAz)×(exBx+eyBy+ezBz)=ex(AyBz−AzBy)+ey(AzBz−AzBz)+ez(AxBy−AyBz)=∣∣∣∣∣∣∣∣∣∣exAxBxeyAyByezAzBz∣∣∣∣∣∣∣∣∣∣
位置矢量:r=exx+eyy+ezz
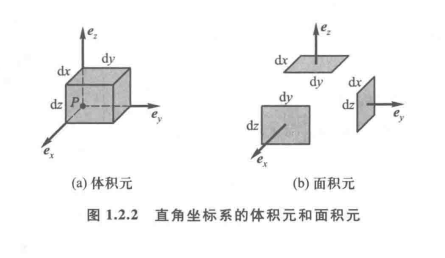
微分元矢量(线元矢量):dl=exdx+eydy+ezdz
面元矢量:
dSx=exdlydlz=exdydzdSy=eydlxdlz=eydxdzdSz=ezdlxdly=ezdxdy
体积元:dV=dxdydz
1.2.2 圆柱坐标系
三个坐标量的变化范围:
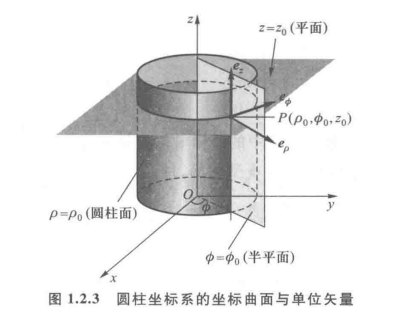
与直角坐标系的变换关系:ρ=x2+y2,ϕ=arctan(y/x),z=z或x=ρcosϕ,y=ρsinϕ,z=z
右手螺旋法则:$\boldsymbol{e}\rho\times\boldsymbol{e}\phi=\boldsymbol{e}z,\boldsymbol{e}\phi\times\boldsymbol{e}z=\boldsymbol{e}\rho,\boldsymbol{e}z\times\boldsymbol{e}\rho=\boldsymbol{e}_\phi $
变换关系:$\boldsymbol{e}{\rho}=\boldsymbol{e}{x}\cos\phi+\boldsymbol{e}{y}\sin\phi,\boldsymbol{e}{\phi}=-\boldsymbol{e}{x}\sin\phi+\boldsymbol{e}{y}\cos\phi $
$\boldsymbol{e}{x}=\boldsymbol{e}{\rho}\cos\phi-\boldsymbol{e}{\phi}\sin\phi,\boldsymbol{e}{y}=\boldsymbol{e}{\rho}\sin\phi+\boldsymbol{e}{\phi}\cos\phi $
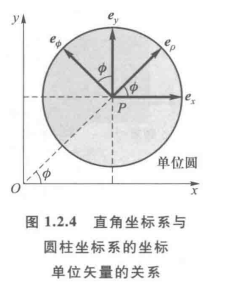
矩阵形式:
⎣⎡eρeϕez⎦⎤=⎣⎡cosϕ−sinϕ0sinϕcosϕ0001⎦⎤⎣⎡e∗e∗e∗⎦⎤⎣⎡eseses⎦⎤=⎣⎡cosϕsinϕ0−sinϕcosϕ0001⎦⎤⎣⎡eρeϕes⎦⎤
必须知道**:圆柱坐标系中的单位矢量eρ和eϕ都不是常矢量**。是随ϕ变化的:
⎩⎪⎪⎪⎪⎨⎪⎪⎪⎪⎧∂ϕ∂eρ=−exsinϕ+eγcosϕ=eϕ∂ϕ∂eϕ=−ezcosϕ−eγsinϕ=−eρ
矢量A在直角坐标系和圆柱坐标系中的变换关系类似上述变换,这里不再赘述。
在圆柱坐标系中,由于eρ和eϕ都是随ϕ变化的,不同点的eρ和eϕ一般是不同的。因此,位于不同点的两个矢量一般不能像直角坐标系那样直接用对应分量进行加法和乘法运算,但对位于同一个点的两个矢量可以用对应分量进行加法和乘法运算。
对位于同一点 P(ρ,ϕ,z)或在同一个 ϕ=常数的平面上的矢量A与B:
A+B=eρ(Aρ+Bρ)+eϕ(Aϕ+Bϕ)+ez(Az+Bz)A⋅B=(eρAρ+eϕAϕ+ezAz)⋅(eρBρ+eϕBϕ+ezBz)=AρBρ+AϕBϕ+AzBzA×B=(eρAρ+eϕAϕ+ezAz)×(eρBρ+eϕBϕ+ezBz)=eρ(AϕBz−AzBϕ)+eϕ(AzBρ−AρBz)+ez(AρBϕ−AϕBρ)=∣∣∣∣∣∣eρAρBρeϕAϕBϕezAzBz∣∣∣∣∣∣(1)(2)(3)
位置矢量:r=eρρ+ezz
线元(微分元)矢量:dr=d(eρρ)+d(ezz)=eρdρ+ρdeρ+ezdz=eρdρ+eϕρdϕ+ezdz
面元矢量:
体积元:dV=ρdρdϕdz
度量系数(拉梅系数):hρ=dρdlρ=1,hϕ=dϕdlϕ=ρ,hz=dzdlz=1
1.2.3 球坐标系
三个坐标量变化范围:
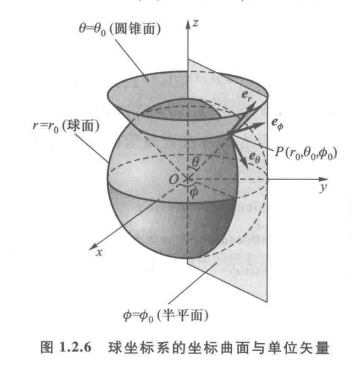
球坐标系与直角坐标系之间的变换关系:r=x2+y2+z2,θ=arccos(z/x2+y2+z2),ϕ=arctan(y/x)或
右手螺旋定则:er×eθ=eϕ,eθ×eϕ=er,eϕ×er=eθ
与直角坐标系变换关系:
⎣⎡ereθeϕ⎦⎤=⎣⎡sinθcosϕcosθcosϕ−sinϕsinθsinϕcosθsinϕcosϕcosθ−sinθ0⎦⎤⎣⎡exeyex⎦⎤⎣⎡exeyez⎦⎤=⎣⎡sinθcosϕsinθsinϕcosθcosθcosϕcosθsinϕ−sinθ−sinϕcosϕ0⎦⎤⎣⎡ereθeϕ⎦⎤
证明使用各个方向投影叠加得到。
其中,单位矢量er,eθ 和 eϕ都不是常矢量,
⎩⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎧∂θ∂er=eθ,∂ϕ∂er=eϕsinθ∂θ∂eθ=−er,∂ϕ∂eθ=eϕcosθ∂θ∂eϕ=0,∂ϕ∂eϕ=−e,sinθ−eϕcosθ
矢量在球坐标系和直角坐标系中的表达式之间的变换关系与上述单位向量之间的关系相同。
对位于同一点 P(r,θ,ϕ)或在沿同一条半径线上的两个矢量 A和B:
A×BA+B=er(Ar+Br)+eθ(Aθ+Bθ)+eϕ(Aϕ+Bϕ)A⋅B=ArBr,+AθBθ+AϕBϕ=er(AθBϕ−AϕBθ)+eθ(AϕBr−ArBϕ)+eϕ(ArBθ−AθBr)=∣∣∣∣∣∣e,ArBreθAθBθeϕAϕBϕ∣∣∣∣∣∣(1)(2)(3)
位置矢量:r=er
微分元(线元)矢量:$\mathrm{d}\boldsymbol{r}=\mathrm{d}\left(\boldsymbol{e}_rr\right)=\boldsymbol{e}_r\mathrm{d}r+r\mathrm{d}\boldsymbol{e}r=\boldsymbol{e}r\mathrm{d}r+\boldsymbol{e}\theta r\mathrm{d}\theta+\boldsymbol{e}\phi r\mathrm{sin}\theta\mathrm{d}\phi $
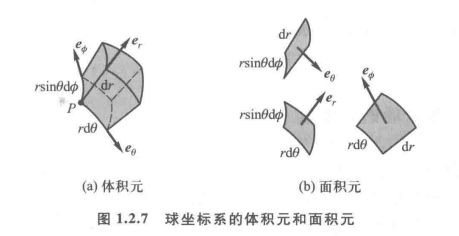
面元矢量(面积元):
体积元:
度量(拉梅)系数:hr=1,hθ=r,hϕ=rsinθ
1.2.4 补充知识
1. 坐标单位矢量之间的变换关系
直角坐标系与圆柱坐标系:
eρeϕezexcosϕ−sinϕ0eysinϕcosϕ0ez001
圆柱坐标系与球坐标系:
ereθeϕeρsinθcosθ0eϕ001ezcosθ−sinθ0
直角坐标系与球坐标系:
ereθeϕexsinθcosϕcosθcosφ−sinϕeysinθsinϕcosθsinϕcosϕezcosθ−sinθ0
2. 单位矢量的空间倒数
极坐标系:
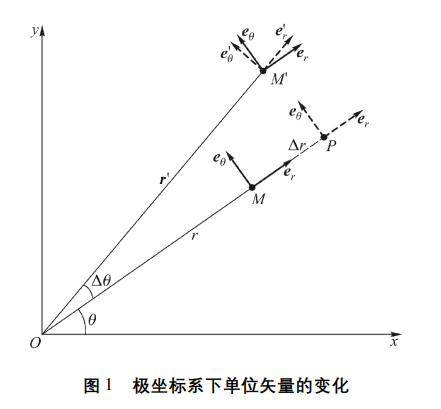
根据偏导数定义:
∂r∂er=Δr→0limΔrer( r+Δr,θ) −er( r,θ)(a)∂θ∂er=Δr→0limΔθer(2r,θ+Δθ)−er(2r,θ)(b)∂r∂eθ=Δr→0limΔreθ(−r+Δr,θ)−eθ(−r,θ)(c)∂θ∂eθ=Δr→0limΔθeθ(1r,θ+Δθ)−eθ(1r,θ)(d)
显然(a)©式当r改变并没有变化,故为0。
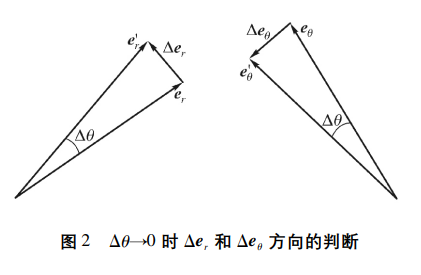
对于(b)(d)式:
∣Δer∣≈∣er∣Δθ=Δθ∣Δeθ∣≈∣eθ∣Δθ=Δθ
可以得到:
∂r∂er∂r∂eθ=0,∂θ∂er=eθ=0,∂θ∂eθ=−er
柱坐标系:
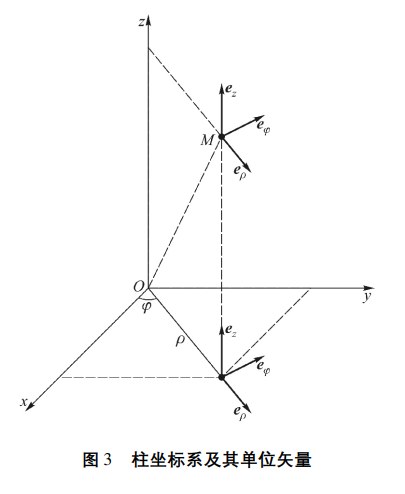
由于单位矢量ez为常矢量,其坐标偏导数均为零,又z变化时只是平移了矢量,故对z的偏导数仍为零:
∂ρ∂eρ∂ρ∂eφ∂ρ∂ez=0,∂φ∂eρ=eφ,∂z∂eρ=0=0,∂φ∂eφ=−eρ,∂z∂eφ=0=0,∂φ∂ez=0,∂z∂ez=0
球坐标系:
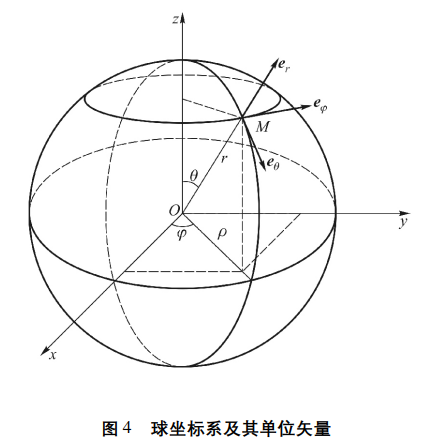
r,θ平面构成平面极坐标系,又eϕ大小和方向不随r和θ变化,可以得出:
∂r∂er=0,∂θ∂er=eθ,∂r∂eθ=0,∂θ∂eθ=−er
∂r∂eφ=0,∂θ∂eφ=0
当ϕ变化时,可投影到ρϕ平面进行求导,最终得到:
⎩⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎧∂θ∂er=eθ,∂ϕ∂er=eϕsinθ∂θ∂eθ=−er,∂ϕ∂eθ=eϕcosθ∂θ∂eϕ=0,∂ϕ∂eϕ=−e,sinθ−eϕcosθ
以上推导参考罗宏超,鞠丽平.微分几何法求解单位矢量的空间导数[J].大学物理,2016,35(12):23-25+41.DOI:10.16854/j.cnki.1000-0712.2016.0175.
该封面图片由katerinavulcova在Pixabay上发布
















