FDTD
FDTD简介
时域有限差分方法基本方程
麦克斯韦方程组
本构关系
DB=εE=μH
把电流密度J写成导体电流密度Jc和施加电流密度Ji之和,同样对磁流密度也就行分解,重写麦克斯韦方程:
∇×H∇×E=ε∂t∂E+σeE+Ji=−μ∂t∂H−σmH−Mi
上面的方程仅设计电磁场E和H,而为涉及通量密度矢量D和B。公式中出现了四个本构关系参量,所以只能描述任意线性、各向同性的媒质。虽然FDTD公式中未出现散度方程,但是可以用来检测仿真结果。
在三维空间中把方程分解为3个标量方程。得到:
∂t∂Ex=εx1(∂y∂Hz−∂z∂Hy−σxeEx−Jix)∂t∂Ey=εy1(∂z∂Hx−∂x∂Hz−σyeEy−Jiy)∂t∂Ez=εz1(∂x∂Hy−∂y∂Hx−σzeEz−Jiz)∂t∂Hx=μx1(∂z∂Ey−∂y∂Ez−σxmHx−Mix)∂t∂Hy=μy1(∂x∂Ex−∂z∂Ex−σymHy−Miy)∂t∂Hz=μz1(∂y∂Ex−∂x∂Ey−σzmHz−Miz)
导数的近似差分
前向差分公式f′(x)≈Δxf(x+Δx)−f(x)
后向差分公式f′(x)≈Δxf(x)−f(x−Δx)
中心差分公式f′(x)≈2Δxf(x+Δx)−f(x−Δx)
其中前向差分和后向差分公式具有一阶精度,但是中心差分公式具有二阶精度。
二阶导数的近似差分
中心差分公式f′′(x)≈(Δx)2f(x+Δx)−2f(x)+f(x−Δx)

三维问题的FDTD更新方程
FDTD 技术将三维问题的几何结构分解为单元,以构成相应的网格。下图示出由(Nx×Ny×Nz)个Yee 单元构成的网格。使用矩形 Yee 单元,以单元的大小作为分辨率,用阶跃或阶梯形式来近似表面和内部几何结构。

下图示出了标志为(i,j,k)的 Yee 单元方式中离散空间各场分量位置。电场分量放置在 Yee 单元各棱的中间,平行于各;磁场分量放置在 Yee 单元各面的中心,平行于各面的法线。
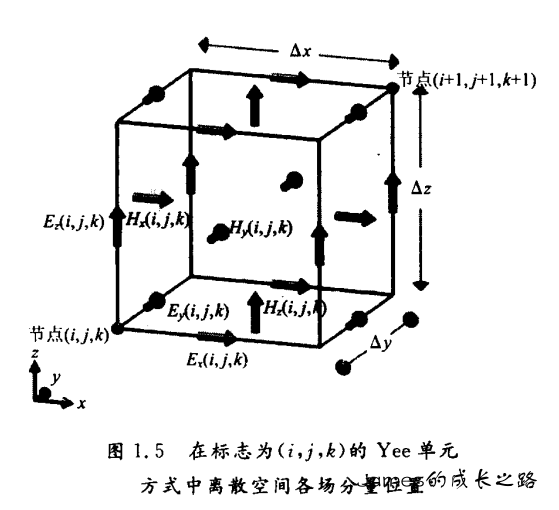
令Yee单元的尺寸分别为Δx,Δy,Δz,可以得到坐标:
Ex(i,j,k)⇒((i−0.5)Δx,(j−1)Δy,(k−1)Δz),Ey(i,j,k)⇒((i−1)Δx,(j−0.5)Δy,(k−1)Δz),Ez(i,j,k)⇒((i−1)Δx,(j−1)Δy,(k−0.5)Δz),Hx(i,j,k)⇒((i−1)Δx,(j−0.5)Δy,(k−0.5)Δz),Hy(i,j,k)⇒((i−0.5)Δx,(j−1)Δy,(k−0.5)Δz),Hz(i,j,k)⇒((i−0.5)Δx,(j−0.5)Δy,(k−1)Δz)。
FDTD算法在离散时间瞬间取样和计算场值,但是电场取样时刻为整数步长时刻,磁场取样为半整数时间步时刻。由于场分量和时间和空间都有关,故用上标表示时间标志。例如:((i−1)Δx,(j−1)Δy,(k−0.5)Δz)记为Ezn(i,j,k)。其他以此类推。
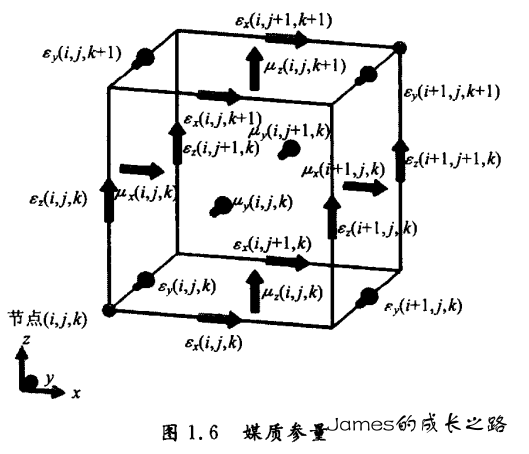
物质参量(介电常数、磁导率、电导率和导磁性)分布在整个 FDTD 网格上,并且与场量相关,因此它们的标记与专场量相同。下图给出了介电常数和磁导率的标记。电导率分布在整个网格,其标记同介电常数。同样,导磁性的标记也与磁导率相同。对离散取样的场分量,在空间和时间上都具备适当的标记方式,这样麦克斯韦方程的旋度方程就可以标量方程的差分形式给出。
考虑方程:∂t∂Ex=εx1(∂y∂Hx−∂z∂Hy−σxeEx−Jiπ)
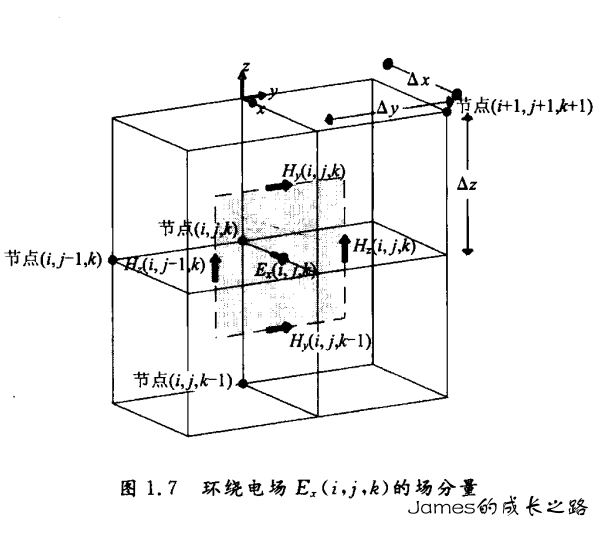
可以写出差分形式
ΔtExn+1(i,j,k)−Exn(i,j,k)=εx(i,j,k)1ΔyHzn+21(i,j,k)−Hzn+21(i,j−1,k)−εx(i,j,k)1ΔyHyn+21(i,j,k)−Hyn+21(i,j,k−1)−εx(i,j,k)σxe(i,j,k)Exn+21(i,j,k)−εx(i,j,k)∫ixn+21(i,j,k)
上式右边包含的电场是半整数时刻的,,这些电场可写为两个整数时刻的平均。Exn+21(i,j,k)=2Exn+1(i,j,k)+Exn(i,j,k)
由上面两式可以推出FDTD更新方程:
Exn+1(i,j,k)=2εx(i,j,k)+Δtσxe(i,j,k)2εx(i,j,k)−Δtσxe(i,j,k)Exn(i,j,k)+(2εx(i,j,k)+Δtσxe(i,j,k))Δy2Δt(Hzn+21(i,j,k)−Hzn+21(i,j−1,k))−(2εr(i,j,k)+Δtσre(i,j,k))Δz2Δt(Hyn+21(i,j,k)−Hyn+21(i,j,k−1))−2εx(i,j,k)+Δtσxϵ(i,j,k)2ΔtJx˙n+21(i,j,k)
上式表明了如何用用过去时刻的电场/磁场分量和激励分量来计算下一时间步的电场分量。同样可以推出其他分量的更新方程。
对于磁场考虑方程∂t∂Hx=μx1(∂z∂Ey−∂y∂Hz−σxmHx−Mix)
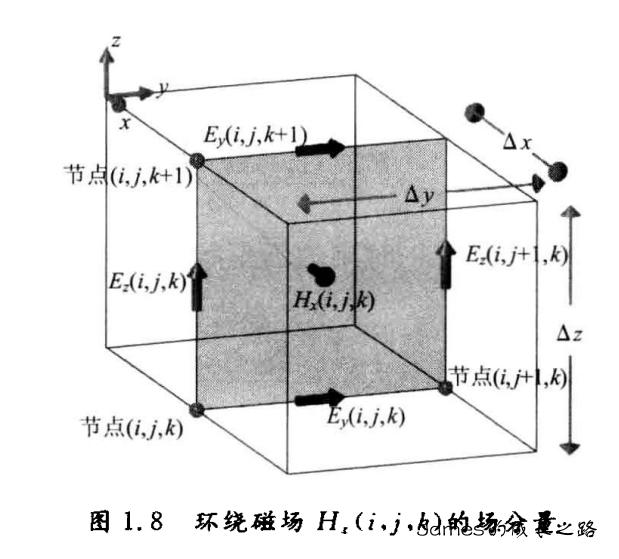
写出差分形式:
ΔtHxn+21(i,j,k)−Hxn−21(i,j,k)=μx(i,j,k)1ΔzEyn(i,j,k+1)−Eyn(i,j,k)−μx(i,j,k)1ΔyEzn(i,j+1,k)−Ezn(i,j,k)−μx(i,j,k)σxm(i,j,k)Hxn(i,j,k)−μx(i,j,k)1Mixn(i,j,k)
整理之后同样可以得到磁场的更新公式
Hxn+21(i,j,k)=2μx(i,j,k)−Δtσxm(i,j,k)2μx(i,j,k)−Δtσxm(i,j,k)Hxn−21(i,j,k)+(2μx(i,j,k)+Δtσxm(i,j,k))Δz2Δt(Eyn(i,j,k+1)−Eyn(i,j,k))−(2μx(i,j,k)+Δtσxm(i,j,k))Δy2Δt(Ezn(i,j+1,k)−Ezn(i,j,k))−2μx(i,j,k)+Δtσxn(i,j,k)2ΔtMixn(i,j,k)
同样可以推出其他分量的更新方程。
最后,引入系数项,可以得到
Exn+1(i,j,k)=Cexe(i,j,k)×Exn(i,j,k)+Cexhz(i,j,k)×(Hzn+21(i,j,k)−Hzn+21(i,j−1,k))+Cexhy(i,j,k)×(Hyn+21(i,j,k)−Hyn+21(i,j,k−1))+Cexj(i,j,k)×Jixn+21(i,j,k),
式中
Cexe(i,j,k)Cexhz(i,j,k)Cexhy(i,j,k)Cexj(i,j,k)=2εx(i,j,k)+Δtσxe(i,j,k)2εx(i,j,k)−Δtσxe(i,j,k),=(2εx(i,j,k)+Δtσxe(i,j,k))Δy2Δt,=−(2εx(i,j,k)+Δtσxe(i,j,k))Δz2Δt,=−2εx(i,j,k)+Δtσxe(i,j,k)2Δt.
Eyn+1(i,j,k)=Ceye(i,j,k)×Eyn(i,j,k)+Ceyhx(i,j,k)×(Hxn+21(i,j,k)−Hxn+21(i,j,k−1))+Ceyhz(i,j,k)×(Hzn+21(i,j,k)−Hzn+21(i−1,j,k))+Ceyj(i,j,k)×Jiyn+21(i,j,k),
式中
Cеуе(i,j,k)Cеуhx(i,j,k)Cеуhz(i,j,k)Ceyj(i,j,k)=2εy(i,j,k)+Δtσye(i,j,k)2εy(i,j,k)−Δtσye(i,j,k),=(2εy(i,j,k)+Δtσye(i,j,k))Δz2Δt,=−(2εy(i,j,k)+Δtσye(i,j,k))Δx2Δt,=−2εy(i,j,k)+Δtσye(i,j,k)2Δt.
Ezn+1(i,j,k)=Ceze(i,j,k)×Ezn(i,j,k)+Cezhy(i,j,k)×(Hyn+21(i,j,k)−Hyn+21(i−1,j,k))+Cezhx(i,j,k)×(Hxn+21(i,j,k)−Hxn+21(i,j−1,k))+Cezj(i,j,k)×Jizn+21(i,j,k),
式中
Ceze(i,j,k)Cezhy(i,j,k)Cezhx(i,j,k)Cezj(i,j,k)=2εz(i,j,k)+Δtσze(i,j,k)2εz(i,j,k)−Δtσze(i,j,k),=(2εz(i,j,k)+Δtσze(i,j,k))Δx2Δt,=−(2εz(i,j,k)+Δtσze(i,j,k))Δy2Δt,=−2εz(i,j,k)+Δtσze(i,j,k)2Δt.
Hxn+21(i,j,k)=Chxh(i,j,k)×Hxn−21(i,j,k)+Chxey(i,j,k)×(Eyn(i,j,k+1)−Eyn(i,j,k))+Chxez(i,j,k)×(Ezn(i,j+1,k)−Ezn(i,j,k))+Chxm(i,j,k)×Mixn(i,j,k),
式中
Chxh(i,j,k)=2μx(i,j,k)+Δtσxm(i,j,k)2μx(i,j,k)−Δtσxm(i,j,k),Chхеу(i,j,k)=(2μx(i,j,k)+Δtσxm(i,j,k))Δz2Δt,Chxez(i,j,k)=−(2μx(i,j,k)+Δtσxm(i,j,k))Δy2Δt,Chxm(i,j,k)=−2μx(i,j,k)+Δtσxm(i,j,k)2Δt.
Hyn+21(i,j,k)=Chyh(i,j,k)×Hyn−21(i,j,k)+Chyez(i,j,k)×(Ezn(i+1,j,k)−Ezn(i,j,k))+Chyex(i,j,k)×(Exn(i,j,k+1)−Exn(i,j,k))+Chym(i,j,k)×Miyn(i,j,k)
式中
Chyh(i,j,k)=2μy(i,j,k)+Δtσym(i,j,k)2μy(i,j,k)−Δtσym(i,j,k),Chyez(i,j,k)=(2μy(i,j,k)+Δtσym(i,j,k))Δx2Δt,Cbуех(i,j,k)=−(2μy(i,j,k)+Δtσym(i,j,k))Δz2Δt,Chym(i,j,k)=−2μy(i,j,k)+Δtσym(i,j,k)2Δt.
Hzn+21(i,j,k)=Chzh(i,j,k)×Hzn−21(i,j,k)+Chzex(i,j,k)×(Exn(i,j+1,k)−Exn(i,j,k))+Chzey(i,j,k)×(Eyn(i+1,j,k)−Eyn(i,j,k))+Chzm(i,j,k)×Mizn(i,j,k),
式中
Chzh(i,j,k)=2μz(i,j,k)+Δtσzm(i,j,k)2μy(i,j,k)−Δtσzm(i,j,k),Chzex(i,j,k)=(2μz(i,j,k)+Δtσzm(i,j,k))Δy2Δt,Chzey(i,j,k)=−(2μz(i,j,k)+Δtσzm(i,j,k))Δx2Δt,Chzm(i,j,k)=−2μz(i,j,k)+Δtσzm(i,j,k)2Δt.
应该注意的是,在所有系数项中,第一、二个系数下标与更新的场量相关,而对三个下标系数,第三个下标与所乘的场或源相关,对四下标系数,第三个和第四个下标与所乘的场量相关。
推导出FDTD的更新公式之后,就可以构造出时间步进算法。流程图如下:

二维问题的FDTD迭代方程
在二维情况下,场仅在一维方向分布时,可以得到简化的二维方程:
∂t∂Ex=εx1(∂y∂Hz−σx′Ex−Jix)∂t∂Ey=εy1(−∂x∂Hz−σyeEy−Jiy)∂t∂Ez=εz1(∂x∂Hy−∂y∂Hx−σzeEz−Jiz)∂t∂Hx=μx1(−∂y∂Ez−σxmHx−Mix)∂t∂Hy=μy1(∂x∂Ez−σymHy−Miy)∂t∂Hz=μz1(∂y∂Ez−∂x∂Ey−σzmHz−Miz)
可将上面的方程根据场量对z方向的关系分为两组,即TMz模式和TEz模式。可以对这两类问题分别求解,问题的全解可以由这两类解的和来得到。
TEz模式
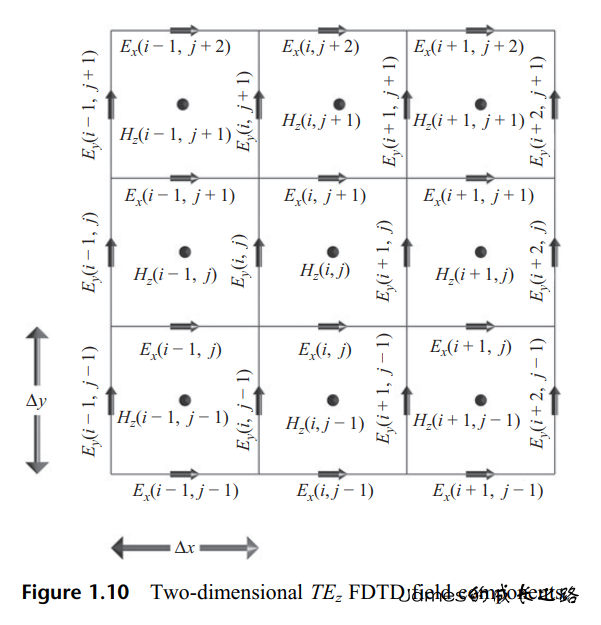
FDTD更新方程:
Exn+1(i,j)=Cexe(i,j)×Exn(i,j)+Cexhz(i,j)×(Hzn+21(i,j)−Hzn+21(i,j−1))+Cexj(i,j)×Jixn+21(i,j),
式中
Cexe(i,j)=2εx(i,j)+Δtσxe(i,j)2εx(i,j)−Δtσxe(i,j),Cexhz(i,j)=(2εx(i,j)+Δtσxe(i,j))Δy2Δt,Cexj(i,j)=−2εx(i,j)+Δtσxe(i,j)2Δt.
Eyn+1(i,j)=Ceye(i,j)×Eyn(i,j)+Ceyhz(i,j)×(Hzn+21(i,j)−Hzn+21(i−1,j))+Ceyj(i,j)×Jiyn+21(i,j),
式中
Ceye(i,j)=2εy(i,j)+Δtσye(i,j)2εy(i,j)−Δtσye(i,j),Ceyhz(i,j)=−(2εy(i,j)+Δtσye(i,j))Δx2Δt,Ceyj(i,j)=−2εy(i,j)+Δtσνe(i,j)2Δt.
Hzn+21(i,j)=Chzh(i,j)×Hzn−21(i,j)+Cbzex(i,j)×(Exn(i,j+1)−Exn(i,j))+Chzey(i,j)×(Eyn(i+1,j)−Eyn(i,j))+Chzm(i,j)×Mizm(i,j),
式中
Chzh(i,j)=2μz(i,j)+Δtσzm(i,j)2μz(i,j)−Δtσzm(i,j),Chzex(i,j)=(2μz(i,j)+Δtσzm(i,j))Δy2Δt,Chzey(i,j)=−(2μz(i,j)+Δtσzm(i,j))Δx2Δt,Chzm(i,j)=−2μz(i,j)+Δtσzm(i,j)2Δt.
TMz模式
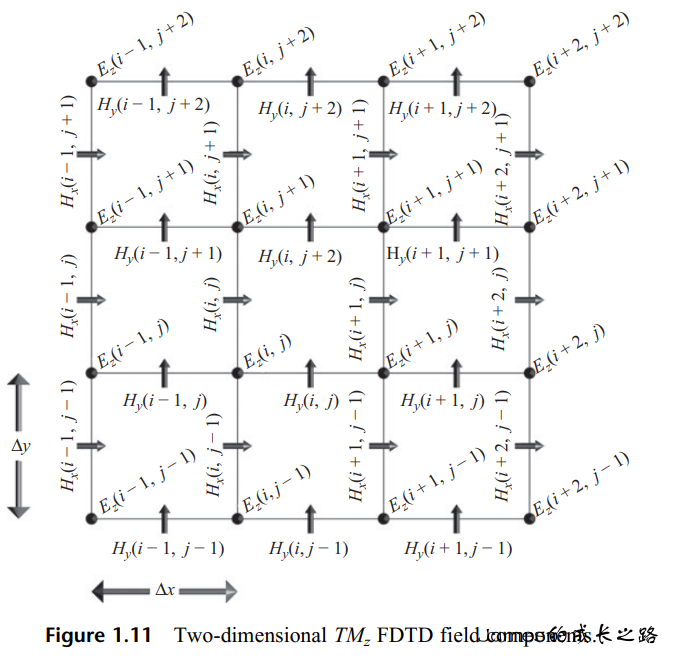
Ezn+1(i,j)=Ceze(i,j)×Ezn(i,j)+Cezhy(i,j)×(Hyn+21(i,j)−Hyn+21(i−1,j))+Cezhx(i,j)×(Hxn+21(i,j)−Hxn+21(i,j−1))+Cezj(i,j)×Jizn+21(i,j),
式中
Ceze(i,j)Cezhy(i,j)Cezhx(i,j)Cezj(i,j)=2εz(i,j)+Δtσze(i,j)2εz(i,j)−Δtσze(i,j),=(2εz(i,j)+Δtσze(i,j))Δx2Δt,=−(2εz(i,j)+Δtσze(i,j))Δy2Δt,=−2εz(i,j)+Δtσze(i,j)2Δt.
Hxn+21(i,j)=Chxh(i,j)×Hxn−21(i,j)+Chxez(i,j)×(Ezn(i,j+1)−Ezn(i,j))+Chxm(i,j)×Mixn(i,j),
式中
Chxh(i,j)=2μx(i,j)+Δtσxm(i,j)2μx(i,j)−Δtσxm(i,j),Chxez(i,j)=−(2μx(i,j)+Δtσxm(i,j))Δy2Δt,Chxm(i,j)=−2μx(i,j)+Δtσxm(i,j)2Δt.
一维FDTD问题的更新方程
一维情况下,场分布与两个坐标变量无关。此时麦克斯韦方程可以重写为:
∂t∂Ex=εx1(−σxeEx−Jix),(1.39a)∂t∂Ey=εy1(−∂x∂Hz−σyeEy−Jiy),(1.39b)∂t∂Ez=εz1(∂x∂Hy−σzeEz−Jiz),(1.39c)∂t∂Hx=μx1(−σxmHx−Mix),(1.39d)∂t∂Hy=μy1(∂x∂Ez−σymHy−Miy),(1.39e)∂t∂Hz=μz1(−∂x∂Ey−σzmHz−Miz).(1.39f)
上式第一个和第四个方程不包含对空间的导数的项,因此这两式子不代表传播场。而其他方程对于x轴属于横向场,因此,在一维的情况下存在TEM波,其传播如同平面波的传播。
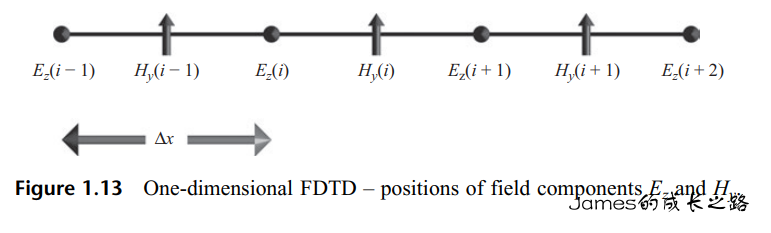
分析一维场的时候采用和二维场同样的方法把波分解为两类分离的类型。因为方程(1.39b)和方程(1.39f)仅含Ez和Hx两项,它们与方程(1.39c)方程(1.39e)是去耦合的。后者只含有E,和H两项。对方程(1.39b)和方程(1.39f),场量的空间位置如下图所示。
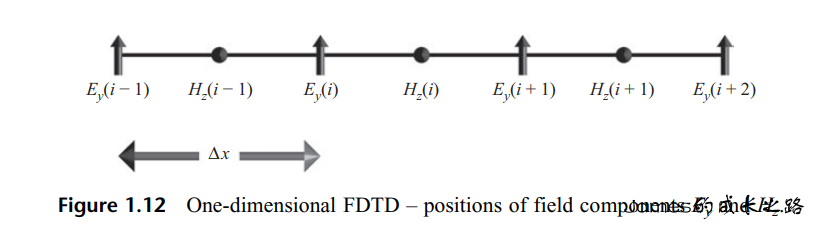
根据中心差分方法可得到FDTD的更新方程:
Eyn+1(i)=Ceye(i)×Eyn(i)+Ceyhz(i)×(Hzn+21(i)−Hzn+21(i−1))+Ceyj(i)×Jiyn+21(i),
式中
Ceye(i)=2εy(i)+Δtσye(i)2εy(i)−Δtσye(i),Ceyhz(i)=−(2εy(i)+Δtσye(i))Δx2Δt,Ceyj(i)=−2εy(i)+Δtσye(i)2Δt,
Hzn+21(i)=Chzh(i)×Hzn−21(i)+Chzey(i)×(Eyn(i+1)−Eyn(i))+Chzm(i)×Mizn(i),(1.41)
式中
Chzh(i)=2μz(i)+Δtσzm(i)2μz(i)−Δtσzm(i),Chzey(i)=−(2μz(i)+Δtσzm(i))Δx2Δt,Chzm(i)=−2μz(i)+Δtσzm(i)2Δt.
对于方程(1.39c)和(1.39e),场量的空间位置如图:
FDTD更新方程:
Ezn+1(i)=Ceze(i)×Ezn(i)+Cezhy(i)×(Hyn+21(i)−Hyn+21(i−1))+Cezj(i)×Jizn+21(i),
其中
Ceze(i)=2εz(i)+Δtσze(i)2εz(i)−Δtσze(i),Cezhy(i)=(2εz(i)+Δtσze(i))Δx2Δt,Cezj(i)=−2εz(i)+Δtσze(i)2Δt,
Hyn+21(i)=Chyh(i)×Hyn−21(i)+Chyez(i)×(Ezn(i+1)−Ezn(i))+Chym(i)×Miyn(i),
式中
Chyh(i)=2μy(i)+Δtσym(i)2μy(i)−Δtσym(i),Chyez(i)=(2μy(i)+Δtσym(i))Δx2Δt,Chym(i)=−2μy(i)+Δtσym(i)2Δt.
数值稳定性和色散
在FDTD中,取样的周期应遵循一定的规则,确保解的稳定性。
时域算法中的稳定性
对于一个简单的波方程∂t∂u(x,t)+∂x∂u(x,t)=0,u(x,t=0)=u0(x),其解析解为u(x,t)=u0(x−t)。离散化后得到时域数值算法。
2Δtuin+1−uin−1+2Δxui−1n−ui+1n=0整理后得到uin+1=uin−1+λ(ui+1n−ui−1n)=0,λ=ΔxΔt
下图是一系列表示时间和空间的网格,假定对u,在时间标记为 n 和(n−1)的时刻是已知的。为简单起见,假定所有这些值都为零。还假定,在时间标注为n 时,空间下标为时i,有一小的误差量,用ε来表示。当时间向前推进时,u在(n+1)的值,用上面的递推式可以由低两行的相应值算出。



因此,上述递推式的稳定是有条件的。
FDTD方法的CFL稳定条件
FDTD方法的数值稳定由CFL条件确定。要求时间增量Δt相对于空间网格小于一特定值
Δt⩽c(Δx)21+(Δy)21+(Δz)211其中,c为自由空间光速。
对立方体网格有,Δx=Δy=Δz,则CFL条件变为Δt⩽c3Δx。
一维情况下,CFL条件简化为Δt⩽Δx/c。表明,在一个时间步长内,不容许波行进距离超过一个网格尺寸。
稳定性问题的存在表明,当FDTD迭代进行时,在问题空间可能激励出虚假的收敛场。
数值色散
用FDTD数值方法得到的相速与实际的相速之间的差别称为数值色散。
解析解的色散关系kx2=ω2μ0ε0=(cω)2
在一维情况下,离散后可以推的色散关系[cΔt1sin(2ωΔt)]2=[Δx1sin(2kxΔx)]2
两者是不一样的,这意味着存在与实际解的偏差,这就是由数值解带来的误差。
二维色散关系是[cΔt1sin(2ωΔt)]2=[Δx1sin(2kxΔx)]2+[Δy1sin(2kyΔy)]2
三维色散关系是
在Yee网格中创建目标
目标的定义
在FDTD算法中,开始 FDTD 时间步进迭代之前,第一步应该创建问题。问题的创建需要运行两个子程序:一是定义问题的子程序;二是初始化问题空间和 FDTD参量的子程序。问题的定义过程包括创建数据结构和存储与要解的电磁问题相关的构成信息。其中信息部分包括:在问题空间中的目标几何形状;构成材料的类型;材料的电磁特性;激励源的类型和波形;由 FDTD 所得仿真结果的类型;其他定义 FDTD算法的参量。如时间步数、问题边界的类型。初始化处理将结构数据嵌入到 FDTD媒质网格中,并构造和初始化数据。这包括 FDTD更新参量数组、场的系数数组和在 FDTD 迭代中及选代后用到的数据。简而言之,它为 FDTD计算和后处理准备数据结构。
定义问题空间参量
在问题空间中定义目标
媒质近似
近似策略:假定,每一种媒质位于一个网格单元的中心。这些网格与FDTD网格之间有一定的位置偏移,称为媒质网格。
点留驻方法:粗略近似加权体积平均。Yee单元中的每一媒质单元划分为8个子网格。
可以得到εz(i,j,k)=8ε1+ε2+ε3+ε4+ε5+ε6+ε7+ε8
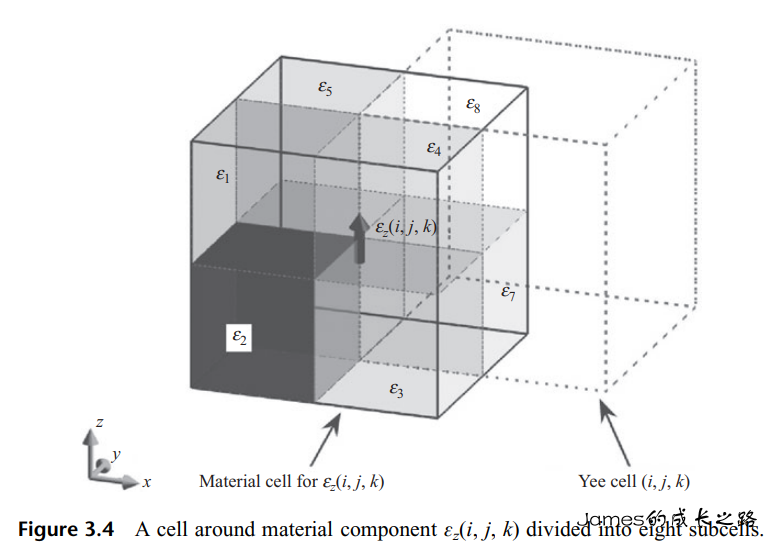
切向和法向分量的子网格平均方案
计算媒质分量平行于两种媒质的界面的等效介电常数ε1A1+ε2A2=εeff×(A1+A2)⇒εeff=εeff(i,j,k)=A1+A2ε1A1+ε2A2
计算媒质分量垂直于两种媒质的界面的等效介电常数εeff=εz(i,j,k)=l1ε2+l2ε1ε1ε2(l1+l2)
可以证明,其他物质参量仍满足这种关系,例如等效磁导率μ小电导率σe和小电导率σm
定义目标
定义零厚度PEC目标
任意环绕着并与PEC平板共线的电导分量都可以指定为PEC电导率,以便模拟似零厚度的PEC平板。
创建媒质网格
改善8个网络平均
有源和无源集总参数电路
FDTD中集总参数元件的更新公式
电压源
节点(i,j,k)和(i,j,k+1)之间极化方向为z正向的电压源的FDTD更新方程
Ezn+1(i,j,k)=Ceze(i,j,k)×Ezn(i,j,k)+Cezhy(i,j,k)×(Hyn+21(i,j,k)−Hyn+21(i−1,j,k))+Cezhx(i,j,k)×(Hxn+21(i,j,k)−Hxn+21(i,j−1,k))+Cezs(i,j,k)×Vsn+21(i,j,k),
式中
Ceze(i,j,k)Cezhy(i,j,k)Cezhx(i,j,k)Cezs(i,j,k)=2εz(i,j,k)+Δtσze(i,j,k)+RsΔxΔyΔtΔz2εz(i,j,k)−Δtσze(i,j,k)−RsΔxΔyRsΔxΔy,=(2εz(i,j,k)+Δtσze(i,j,k)+RsΔxΔyΔtΔz)Δx2Δt,=−(2εz(i,j,k)+Δtσze(i,j,k)+RsΔxΔyΔtΔz)Δy2Δt,=−(2εz(i,j,k)+Δtσze(i,j,k)+RsΔxΔyΔtΔz)(RsΔxΔy)2Δt,
硬激励电压源
无内阻电压源
Ceze(i,j,k)=−1,Cezhy(i,j,k)=0,Cezhx(i,j,k)=0,Cezs(i,j,k)=−Δz2.
电流源
Ezn+1(i,j,k)=Ceze(i,j,k)×Ezn(i,j,k)+Cezhy(i,j,k)×(Hyn+21(i,j,k)−Hyn+21(i−1,j,k))+Cezhx(i,j,k)×(Hxn+21(i,j,k)−Hxn+21(i,j−1,k))+Cezs(i,j,k)×Isn+21(i,j,k),
式中
Ceze(i,j,k)=2εz(i,j,k)+Δtσze(i,j,k)+RsΔxΔyΔtΔz2εz(i,j,k)−Δtσze(i,j,k)−RsΔxΔyΔtΔz,Cezhy(i,j,k)=(2εz(i,j,k)+Δtσze(i,j,k)+RsΔxΔyΔtΔz)Δx2Δt,Cezhx(i,j,k)=−(2εz(i,j,k)+Δtσze(i,j,k)+RsΔxΔyΔtΔz)Δy2Δt,Cezs(i,j,k)=−(2εz(i,j,k)+Δtσze(i,j,k)+RsΔxΔyΔtΔz)ΔxΔy2Δt,
电阻的FDTD建模
Ez+1(i,j,k)=Ceze(i,j,k)×Ezn(i,j,k)+Cezhy(i,j,k)×[Hyn+21(i,j,k)−Hyn+21(i−1,j,k)]+Cezhz(i,j,k)×[Hzn+21(i,j,k)−Hzn+21(i,j−1,k)]
式中
Cϵϵϵ(i,j,k)=2εϵ(i,j,k)+Δtσϵ∗(i,j,k)+RΔxΔyΔtΔz2εϵ(i,j,k)−Δtσϵϵ(i,j,k)−RΔxΔyΔtΔzCϵthy(i,j,k)=[2εϵ(i,j,k)+Δtσϵϵ(i,j,k)+RΔxΔyΔtΔz]Δx˙2ΔtCϵ∗h∗(i,j,k)=[2εϵ(i,j,k)+Δtσϵϵ(i,j,k)+RΔxΔyΔtΔx]Δy2Δt
电容的FDTD建模
Ezn+1(i,j,k)=Ceze(i,j,k)×Ezn(i,j,k)+Cezhy(i,j,k)×(Hyn+21(i,j,k)−Hyn+21(i−1,j,k))+Cezhx(i,j,k)×(Hxn+21(i,j,k)−Hxn+21(i,j−1,k)),
式中
Ceze(i,j,k)=2εz(i,j,k)+Δtσze(i,j,k)+ΔxΔy2CΔz2εz(i,j,k)−Δtσze(i,j,k)+ΔxΔy2CΔz,Cezhy(i,j,k)=(2εz(i,j,k)+Δtσze(i,j,k)+ΔxΔy2CΔz)Δx2Δt,Cezhx(i,j,k)=−(2εz(i,j,k)+Δtσze(i,j,k)+ΔxΔy2CΔz)Δy2Δt.
电感的FDTD建模
Ezn+1(i,j,k)=Ceze(i,j,k)×Ezn(i,j,k)+Cezhy(i,j,k)×(Hyn+21(i,j,k)−Hyn+21(i−1,j,k))+Cezhx(i,j,k)×(Hxn+21(i,j,k)−Hxn+21(i,j−1,k))+Cezj(i,j,k)×Jizn+21(i,j,k),
式中
Jizn+21(i,j,k)=Jizn−21(i,j,k)+LΔxΔyΔtΔzEzn(i,j,k).
Ceze(i,j,k)=2εz(i,j,k)+Δtσze(i,j,k)2εz(i,j,k)−Δtσze(i,j,k),Cezhy(i,j,k)==(2εz(i,j,k)+Δtσze(i,j,k))Δx2Δt,Cezhx(i,j,k)=−(2εz(i,j,k)+Δtσze(i,j,k))Δy2Δt,Cezj(i,j,k)=−2εz(i,j,k)+Δtσze(i,j,k)2Δt.
位于表明或体积内的集总参数元件
电阻R′=R×rke−rks(rie−ris+1)×(rje−rjs+1)
电感L′=L×ke−ks(ie−is+1)×(je−js+1)
电容C′=C×(ie−is+1)×(je−js+1)ke−ks
二极管的FDTD模拟
正向放置的二极管
AeBr+x+C=0
式中
C=Ceze(i,j,k)×Ezn(i,j,k)+Cezhy(i,j,k)×(Hyn+21(i,j,k)−Hyn+21(i−1,j,k)+Cezhx(i,j,k)×(Hxn+21(i,j,k)−Hxn+21(i,j−1,k))+Cezd(i,j,k),Ceze(i,j,k)=−2εz(i,j,k)+Δtσze(i,j,k)2εz(i,j,k)−Δtσze(i,j,k),Cezhy(i,j,k)=−(2εz(i,j,k)+Δtσze(i,j,k))Δx2Δt,Cezhx(i,j,k)=(2εz(i,j,k)+Δtσze(i,j,k))Δy2Δt,Cezd(i,j,k)=−2εz(i,j,k)ΔxΔy+Δtσze(i,j,k)ΔxΔy2ΔtI0.
解此方程可用Newton-Raphson法,由于在连续时间步长内变化很小,所以只需要几次迭代就可以接近目标值。
反向放置的二极管
AeBx+x+C=0
式中
C=Ceze(i,j,k)×Ezn(i,j,k)+Cezhy(i,j,k)×(Hyn+21(i,j,k)−Hyn+21(i−1,j,k))+Cezhx(i,j,k)×(Hxn+21(i,j,k)−Hxn+21(i,j−1,k))+Cezd(i,j,k),Ceze(i,j,k)=−2εz(i,j,k)+Δtσze(i,j,k)2εz(i,j,k)−Δtσze(i,j,k),Cezhy(i,j,k)=−(2εz(i,j,k)+Δtσze(i,j,k))Δx2Δt,Cezhx(i,j,k)=(2εz(i,j,k)+Δtσze(i,j,k))Δy2Δt,Cezd(i,j,k)=2εz(i,j,k)ΔxΔy+Δtσze(i,j,k)ΔxΔy2ΔtI0.
集总参数元件的定义、初始化和模拟
集总参数元件的定义
FDTD参量和数组的初始化
集总参数元件的初始化
更新系数的初始化
电压源更新系数的初始化
电流源更新系数的初始化
电感更新系数的初始化
电阻更新系数的初始化
电容更新系数的初始化
二极管更新系数的初始化
电场和磁场以及电压和电流的取样
计算取样电压
计算取样电流
输出参数的定义与初始化
初始化输出参量
运行时间中的图形化显示的初始化
运行FDTD模拟:时进循环
磁场更新
电场更新
与电压源相关的电场更新
与电流源相关的电场更新
与电感相关的电场更新:注意需要使用之前时间的参数来更新。
与二极管相关的电场更新
磁场分量取样的获取
取样电流的获取
取样电场分量的获取
取样电压的获取
显示取样参量
显示FDTD模拟结果
激励源的波形与从时域到频域的变换
常用FDTD仿真波形
正弦波形
如果观察电磁问题对正弦波的激励响应,则需要运行足够长的时间,以使瞬态响应中,由于源的开始而激励出的高频信号完全逝去,只留下主正弦信号。
高斯波形
对于大多数应用,在合理的FDTD模拟中,设最高频率波长大于20倍网格尺寸是充分的。
高斯波形g(t)=e−(rt)2,τ为一参数决定高斯脉冲在时域和频域的宽度。其傅里叶变换是G(ω)=τπe−4(πω)2
在FDTD计算中,最高频率由精度参量number of cells wavelength决定:fmax=λminc=n cΔsmaxc式中,c自由空间光速,Δsmax为Δx,Δy,Δz中的最大网格尺寸,λmin为自由空间中最高工作频率波长。
将高斯波形的有效最高频率考虑为其幅度是最高高斯频谱幅度的10%的频率,可以计算出τ=πc2.3ncΔsmax≈2cncΔsmax
时域移动高斯波形g(t)=e−(rr−t0)2,t0为时间移动。
高斯波形的导数归一化
该封面图片由Roland Mey在Pixabay上发布






















